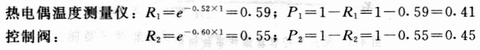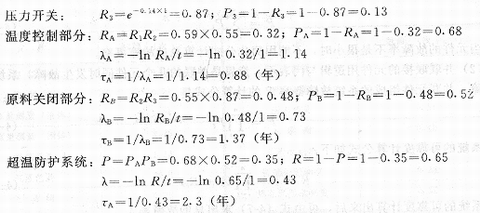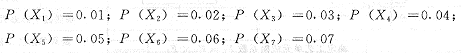二、元件的故障概率及其求法
构成设备或装置的元件,工作一定时间就会发生故障或失效。所谓故障就是指元件、子系统或系统在运行时达不到规定的功能。对可修复系统的失效就是故障。
元件在两次相邻故障间隔期内正常工作的平均时间,叫平均故障间隔期,用τ表示。如某元件在第一次工作时间t1后出现故障,第二次工作时间t2后出现故障,第 n 次工作tn 时间后出现故障,则平均故障间隔期为:

τ一般是通过实验测定几个元件的平均故障间隔时间的平均值得到的。
元件在单位时间(或周期)内发生故障的平均值称为平均故障率,用l表示,单位为故障次数/时间。平均故障率是平均故障间隔期的倒数,即:

故障率是通过实验测定出来的,实际应用时受到环境因素的不良影响,如温度、湿度、振动、腐蚀等,故应给予修正,即考虑一定的修正系数(严重系数是)。部分环境下严重系数 h 的取值见表 4-3。

表 4-3 严重系数值举例

使用场所	k	使用场所	k
实验室	1	火箭试验台	60
普通室	1.1～10	飞 机	80～150
船 舶	10～18	火 箭	400～1000
铁路车辆、牵引式公共汽车	13～30

元件在规定时间内和规定条件下完成规定功能的概率称为可靠度,用 R(t) 表示。元件在时间间隔(0,t)内的可靠度符合下列关系:

式中t ---元件运行时间。
式中t ---元件运行时间。
元件在规定时间内和规定条件下没有完成规定功能(失效)的概率就是故障概率( 或不可靠度),用P(t)表示。故障概率是可靠度的补事件,用下式得到:

式 (4-7) 和式 (4-8) 只适用于故障率l稳定的情况。许多元件的故障率随时间而变化,显示出如图 4-3 所示的浴盆曲线。

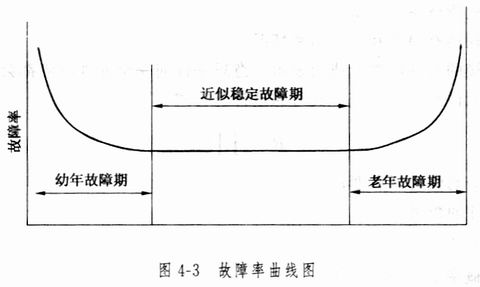
由图可见,元件故障率随时间变化有三个时期,即幼年故障期(早期故障期)、近似稳定故障期( 偶然故障期)和老年故障期(损耗故障期)。元件在幼年期和老年期故障率都很高。这是因为元件在新的时候可能内部有缺陷或在调试过程被损坏,因而开始故障率较高,但很快就下降了。当使用时间长了,由于老化、磨损,功能下降,故障率又会迅速提高。如果设备或元件在老年期之前,更换或修理即将失效部分,则可延长使用寿命。在幼年和老年两个周期之间( 偶然故障期) 的故障率低且稳定, 式(4-7)和式(4-8)都适用。

表 4-4 部分元件的故障率

元件	故障/〈次•a-1)	元件	故障/〈次•a-1〉
控制阅	0.60	压力测量	1.41
控制器	0.29	世压阅	0.022
流量测量〈液体)	1.14	压力开关	0.14
流量测量〈固体〉	3.75	电磁阅	0.42
流量开关	1.12	步进电动机	0.044
气液色谱	30.6	长纸条记录仪	0.22
手动阀	0.13	热电偶温度测量	0.52
指示灯	0.044	温度计温度测量	0.027
液位测量(液体)	1.70	阔动定位器	0.44
液位测量(固体)	6.86
氧分析仪	5.65
pH计	5.88

资料来源: Fank P.Lees, Loss Prevention in the Process Industries(London:Butterworths,1986).

三、元件的联接及系统故障(事故)概率计算

生产装置或工艺过程是由许多元件联接在一起构成的,这些元件发生故障常会导致整个系统故障或事故的发生。因此,可根据各个元件故障概率,依照它们之间的联接关系计算出整个系统的故障概率。
元件的相互联接有串联和并联两种情况。
(1) 串联联接的元件用逻辑或门表示,意思是任何一个元件故障都会引起系统发生故障或事故。串联元件组成的系统,其可靠度计算公式如下:

式中 Ri---每个元件的可靠度;
n ---元件的数量。
系统的故障概率 P 由下式计算:

式中 Pi ---每个元件的故障概率。
只有 A 和 B 两个元件组成的系统,上式展开为:

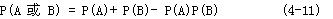
如果元件的故障概率很小,则 P(A)P(B) 项可以忽略,此时式(4-11)可简化为:

式 (4-10) 则可简化为:

当元件的故障率不是很小时,不能用简化公式计算总的故障概率。
(2) 并联联接的元件用逻辑与门表示,意思是并联的几个元件同时发生故障,系统就会故障。并联元件组成的系统故障概率P 的计算公式是:

系统的可靠度计算公式如下:

系统的可靠度计算出来后,可由式(4-7)求出总的故障率λ。

某反应器内进行的是放热反应,当温度超过一定值后,会引起反应失控而爆炸。为及时移走反应热,在反应器外面安装了夹套冷却水系统。由反应器上的热电偶温度测量仪与冷却水进口阀联接,根据温度控制冷却水流量。为防止冷却水供给失效, 在冷却水进水管上安装了压力开关并与原料进口阀联接,当水压小到一定值时,原料进口阀会自动关闭,停止反应。装置组成如图 4-4 所示。试计算这一装置发生超温爆炸的故障率、故障概率、可靠度和平均故障间隔期。假设操作周期为 1 年。

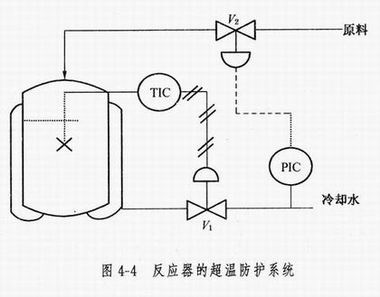
解: 由图得知,反应器的超温防护系统由温度控制和原料关闭两部分组成。温度控制部分的温度测量仪与冷却水进口阀串联,原料关闭部分的压力开关和原料进口阀也是串联的,而温度控制和原料关闭两部分则为并联关系。
由表4-4查得热电偶温度测量、控制阀、压力开关的故障率分别是 0.52、0.60 、0.14次/a 。首先,根据式(4-7)和式(4-8)计算各个元件的可靠度和故障概率。


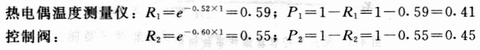
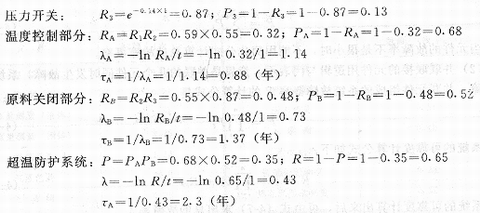
由计算说明,预计温度控制部分每0.88年发生一次故障,原料关闭部分每1.37 年发生一次故障。两部分并联组成的超温防护系统,预计2.3年发生一次故障,防止超温的可靠性明显提高。
计算出安全防护系统的故障率,就可进一步确定反应器超压爆炸的风险率,从而可比较它的安全性。
在事故树分析中,若知道了每个基本事件发生的概率,可求出顶上事件发生概率,根据概率或风险率评价系统的安全性。
下面以图 4-5 所示的事故树为例,说明顶事件发生概率的计算。

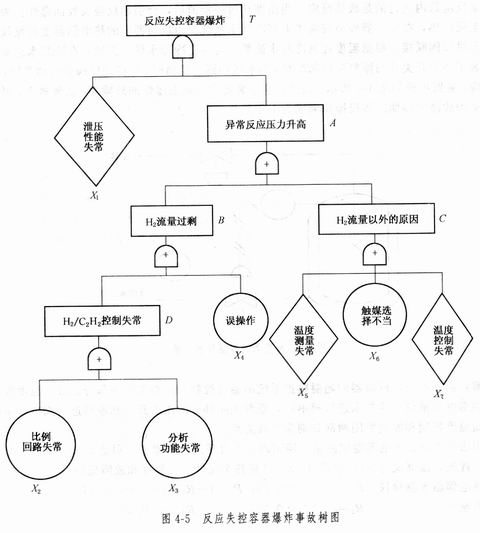
假设事故树中基本事件的故障概率分别是:

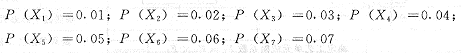
首先求出中间事件 D 的故障概率,逐层向上推算,最后可计算出顶事件的发生概率。

以上是近似计算的结果,各基本事件的故障概率都很小,且事故树中没有重复事件出现。各基本事件故障概率比较大时, 使用式(4-10)计算时应将括号展开。