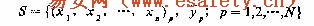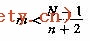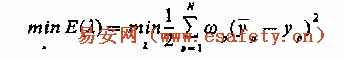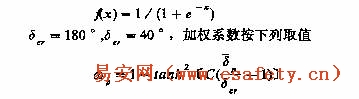引言
电力系统动态安全评价的任务是在某种实际运行方式下对各种预想事故的暂态稳定性在线作出判断。由于一般系统所考虑的预想事故数目较多,因此需要采用快速的暂态稳定分析方法。
早在1983年,IEEE就成立了快速暂态稳定分析工作组,在其报告
(1)中提出过四种方法:暂态能量函数法,模式识别法,改善计算机硬件及采用动态等值。然而,迄今为止,它们都不能满意地用于实际系统的动态安全评价。
传统的数值积分法具有结果准确、可靠的优点,但其缺点是计算速度慢。对此,文献 (2)提出了一种快速数值积分方法,通过分析和试例系统结果表明,对每一预想事故进行暂态稳定分析所需的平均时间比进行一次PQ解耦潮流计算还少,因此对用于实际电力系统的动态安全评价有相当前景。
应用神经网络于电力系统动态安全评价可以大大地减小在线计算工作量。对此,文献 (3)提出采用一种前馈神经网络以得出临界切除时间的方法,但其输人量的获得需要经过大量的附加计算,因而不便于在线应用。本文作者曾在文献(4)中提出以故障前发电机的功率作为输人,故障后某一适当时段内发电机转子间最大相对摇摆角δmax作为输出,用单隐层前馈神经网络进行电力系统动态安全评价的方法。文中论证了其输人与输出之间呈连续映射关系,从而说明神经网络结构的合理性,并同时指出应进一步研究有关样本的获取、隐层神经元的个数及神经网络的训练等间题。
本文将针对这些问题进行比较系统的研究和探讨,提出处理这些问题的原则和方法,并给出两个试例系统的研究结果。
一、用于动态安全评价的神经网络结构原则
进行模式分类和实现数学映射的逼近是前馈神经网络的两个主要功能。电力系统动态安全评价即可以处理为模式分类问题,其输出分为稳定和不稳定两种模式;也可以处理为数学映射的逼近问题,其输出应为表征稳定性的某一连续量,例如最大相对摇摆角δmax或临界切除时间等。这两种处理方法对于训练样本集的要求、神经网络本身的结构及训练方法将有很大的差别。
从对训练样本集的要求来说,处理为模式分类问题将要求在模式空间中稳定与不稳定的边界附近有足够多的样本,而且样本愈接近边界则分类结果愈准确。显然,要获得这样的样本是十分困难的。如果处理为数学映射的逼近间题,则对样本无需上述苛刻要求,但需要在输人空间中取足够数量的点,分别求得其输出量,从而得到足够多的样本,而且要求所得出的样本集能以适当的精度反映输人对输出的映射关系。当然,这就需要进行大量的样本计算,特别是当输人维数较高时,将需要巨大的计算工作量或甚至不现实.然而,对比之下,将动态安全评价处理为映射问题毕竟比处理成模式分类问题简单。
实际上,只要输出量δmax在包含稳定与不稳定的临界值δcr在内的某一适当区间△m=(δcr―δcr,δcr+δcr)内保证一定的精度,便足以满足动态安全评价的要求,而在这一区间以外,输出量可以允许有一定的误差.而且离上述区间愈远,允许的误差可以愈大。δcr根据一般经验可取180o,δcr可在20o~50o间取一适当数值。不难看出,这相当于将动态安全评价问题处理为模式分类与映射的结合。而这样一来,便可以大大地降低对样本集的要求,但为了保证在上述区间内的精度,在样本集中应有相当数量的样本其输出属于区间△m。
在文献(4)中已经证明,当取故障前发电机的功率作为输人,δmax作为输出时,输人对输出将呈连续映射关系。另外,文献(5)已经证明:单隐层、线性输出的前馈神经网络可以在任意精度逼近任何连续映射,只要隐层神经元有足够的数量并且激活函数足够光滑。因此,下面的研究将针对以故障前发电机功率为输人,δmax为输出的单隐层前馈神经网络结构,其映射精度按上述要求。
二、样本集的获取
考虑故障前系统的接线方式、故障地点和类型,以及故障后的操作序列均为给定的情况,在此情况下神经网络只需一个输出单元。其它各种情况将可分别对应于不同的输出单元,或分开采用若干个神经网络.另外,考虑负荷分布情况也已给定,例如系统最大负荷下的负荷分布情况,因为其它负荷分布情况下样本集获取的原则和方法相同。
一般地说,在对输入与输出之间的映射关系无任何先验知识的情况下,只能在输人空间中输人量的取值范围内随机地抽取若干个点组成一个点集,或者对每一个输人量按某种规则确定若干个取值,然后对各个输人量的取值进行组合得出输人空间中的一个点集。依次对每个点求出相应的输出,从而得出一组样本的集合。如用xi表示第i个输人量,输入空间的维数为n,并用表示输出量,则这组个样本的集合可表示为
如果每一个输人取r个不同的数值,则S中的样本数N将多达rn,而为了使样本集能充分地反映输人、输出映射关系,r的取值又不宜太小。这样,在维数n较大的情况下,样本集的计算将需要巨大的工作量.通过随机抽取输人空间中的点而组成样本集,除了方法不同以外,并不能因此而使所需样本的个数非常显著地减少。
其实,如果考虑电力系统运行情况下具体特点,并将动态安全评价问题处理为模式分类与映射的结合,则所需样本的数目可以大大地减少。实际上,电力系统在正常运行情况下,发电机间的功率分配已满足安全性要求,而需要在线动态安全评价的运行情况通常属于一些未能预见的特殊运行情况,例如一些机组在检修的同时另一些机组因偶然事故而停运。这些特殊运行情况可以看成是在正常运行情况的基础上对发电厂间功率分布的调整。然而,因调整而使功率发生较大改变的发电厂数目,加上进行检修和发生故障的发电厂,其总数不可能太多,而绝大多数其它发电厂的功率变化不大。因此,可以根据系统的具体情况及调度运行经验和要求,首先决定需要考虑功率可能发生较大变化的发电厂总数q,并决定各发电厂需要考虑的功率变化范围,再在功率变化范围内按某种规则(例如按一定比例进行均分)分别决定rj个取值。这样,考虑到进行检修、发生故障和对功率作较大调整的各个发电厂可能的组合情况,以及不同的功率取值的相互组合,便可得出输人空间的一组点集。显然,它所包含的总点数最多为

(其中r=max{ri,i=0,1,2,……,n}),这是因为当q-1个电厂的功率取值决定后,第q个电厂的功率便由功率平衡所决定.不难看出,这组点集中己包含了功率变化较大的电厂总数小于q的情况。得出这组输人点集后,便可分别计算相应输出δmax,从而得出一组样本集。
必须指出,上述输人空间点集中的某些点所对应的运行情况可能不满足静态安全要求,或甚至不合理(例如由潮流计算不收敛而说明运行方式不存在),对于这些点需作适当调整或加以剔除。另外,用上述方法得出的样本集中,其输出处于区间△m内及其附近的样本数可能过少,在此情况下,可以采用文献〔6〕所提出的方法,利用δmax的导数方向信息对某些样本的功率分配情况加以调整,以增多输出处于区间△m内的样本,以上便是有关样本获取的原则和方法。
三、隐单元的数目
在前馈神经网络中,隐层神经元的个数对于神经网络的学习和归纳能力有很大的影响。学习能力指神经网络经给定的训练样本集进行训练后,对于训练样本集本身的误差大小,经实际上反映对训练样本集的记忆或复现能力。归纳能力则指经训练后对整个被逼近的映射所呈现的总体误差情况。一般来说,隐单元数过少,神经网络的学习能力不够,而过多的隐单元将使神经网络的归纳能力变差。因此,在训练样本集给定后,隐单元的数目应该选取得当,使它同时具有适当的学习能力和归纳能力。关于隐单元的数目,在现有文献中研究不多,且其结果难以应用。例如文献〔7〕证明,实现任意实值函数的神经网络,其隐单元的最小上界为N-1,平凡下界为1。很明显,这一范围太大。为此,下面提出一种实用的估计方法。
按照一般非线性函数的逼近理论,样本总数应大于待定参数个数。对于n个输人、二个隐单元、单输出的单隐层前馈神经网络,其权和阂值的总数为m (n+2) +1,由此可得:
N>m (n+2)+1
或者
或者
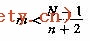
它可作为隐单元数上限的估计。在实际应用中,可以在此范围内通过适当选取不同的隐单元数,对其结果进行比较,最后得到合适的隐单元数。根据本文对两个试例系统的研究结果,取
m+1.5n
对于用作动态安全评价的神经网络来说,是一个很好的估计。
四、神经网络的学习
根据前述将动态安全评价问题处理为模式分类与映射相结合的思想,神经网络的学习是在给定的训练样本集S下,决定神经网络的权和阀值参数(用向量λ表示),使得下列加权误差平方和取极小值
其中,yp为神经网络的实际输出,“,ωp为误差的权值,它可以根据 与区间△m的距离按照一定的规律来决定,距离愈小,所取权值愈大。
对于上式的求解,曾应用经典的BP算法,以及高斯—牛顿法、共轭梯度法、3FGS等算法对试例系统进行过计算,但收敛情况和计算速度都不能令人满意,特别是当n较大时。文献〔8〕给出了一种应用近年来提出的求解非线性最小二乘问题最有效方法—混合GJ-BFGS法进行前馈神经网络学习,并能在学习过程中进行隐单元数自适应调整的方法。本文应用这种方法对两个试验系统进行计算,取得了较好的结果,但也发现隐单元数调整范围不能太大,否则将需要过多的计算时间.然而,如果能对隐单元数给出较好的估计(例如采用式(3)进行估计),则将会取得满意效果。
五、试例系统结果
下面给出两个试例系统的研究结果。一个是文献〔4〕中所用的6机22节点系统,另一个是简化的新英格兰10机39节点系统。
对于6机系统,预想事故为Os,在#11-12线路上发生三相短路,0.12s切除故障线路,对2~5号发电机不同出力分布下的系统进行动态安全评价(1号机取作平衡机,6号机为调相机)。为此,可按前述方法获取252个样本,并作为测试样本集。其中的55个样本构成样本集用于神经网络的训练。
对于10机系统,断开线路6-11,预想事故为Os在#17-16线路上发生三相短路,0.12s切除故障线路,对2-10号发电机不同出力分布下的系统进行动态安全评价(1号机取作平衡机)。同样可得到7793个样本,并作为测试样本集。其中的1000个样本朱用于神经网络的训练。
在进行神经网络训练时,隐单元激活函数取
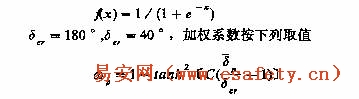
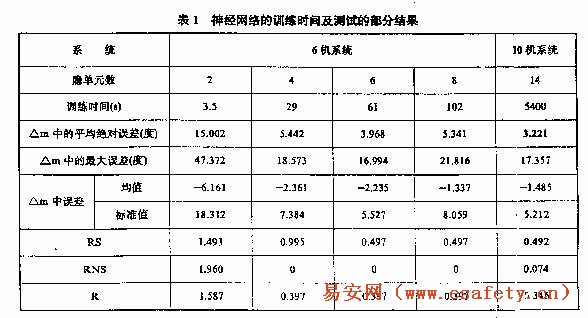
式中,常数C按经验取4.5,对6机系统和10机系统,隐单元数分别取6和14作为初始估计.采用文献〔8〕提出的训练方法进行网络学习,均方误差小于2×10-3时终止训练。表1给出了神经网络的训练时间(用ELXSI - 6400计算机)和对训练好的神经网络进行测试的结果。从表1中可以看出,利用映射和分类相结合的思想,可以在用较少隐单元数的情况下保证△m内映射的精度,进而达到进行动态安全评价的目能,对6机和10机系统分别用6个和14个隐单元可取得几乎最好的归纳能力,这与前面提出的隐单元数估计结果完全一致。由于采用了较先进的训练方法,可使训练时间大大减少。与文献〔4〕中用BP算法训练的结果相比较,由于采用了更合适的隐单元数、更好的训练方法及加权最小二乘法,.所以取得优于以前的结果。
六、结论
在作者以前成果的基础上,本文对前馈神经网络用于电力系统动态安全评价进行了比较系统和更深人的研究。首先提出了将动态安全评价问题处理为模式分类与映射逼近相结合的思想,以减小神经网络的规模。在此基础上,提出了获取样本集的原则和方法,并给出了隐单元数的实用估计方法及处理分类和映射相结合的神经网络加权最小二乘学习。两个试例系统的结果表明了本文提出的思想及各种原则和方法的正确性和有效性。
参考文献
[1] IEEE Report, Rapaid analysis of transient stability, IEEE 8TTII0169-3-PWR, 1987
[2] 杜正春、甘德强、刘玉田、夏道止,基于特殊二阶微分方程数值积分的电力系统动态安全评价,中国电机工程学会电力系统与电网技术综合学术年会论文集1993
[3] D. J. Sobajic, Y. H. Pao, “Ariificial neural-net based dynamic security assessment for electric powersystems”, IEEE Trans. on Power Systems, Vol.4. No. 1, 1989, pp. 220-228
[4] 杜正春、夏道止、‘应用人工神经网络进行电力系统动态安全评价的新方法’.全国高校电自专业第八届年会论文集,1992,南京
[5] G. Cybenki,”Approximation by superposition of a sigmodial function”, Mathematical Contriol Sig-
nals Systems, Vol.2, 1989, pp. 303-314
[6] 杜正春、刘玉田、夏道止,‘一种新的电力系统动态安一评价模式适别方法.,全国高校电自专业第九届年会论文集,1993,重庆
[7] S. C. Huang, Y. F. Huang, ''Bounds on the number of hidden neurons in multilayer perceptrons",IEEE Trans. on Neural Networks, Vol. 2, No. 1, 1991, pp. 47-55
[8] 杜正春、刘玉田、夏道止,‘前馈神经网络学习的混合GN-BFGS法及隐单元数目的自适应调整’,中国神经网络学术大会论文集,1993,西安